Contribution à la montée du niveau des mers
La contribution des calottes polaires à la montée du niveau des mers est essentiellement la combinaison de trois phénomènes : la modification en surface des précipitations neigeuses et de la fonte de glace, à cause du changement climatique et du changement d’altitude du glacier. L’amincissement des plates-formes flottantes, qui fondent par en-dessous à cause du réchauffement de l’océan. La décharge de glace dans l’océan, lorsque la glace s’écoule vers la mer puis se brise en larguant des icebergs.
Modélisation et simulation
Rivière sous-glaciaire gelée en hiverPhoto : Yves Chaux
Surface enneigée d’un glacierPhoto : Yves Chaux
Les processus physiques dans une calotte glaciaire, à l’intérieur comme en surface, sont étudiés par des glaciologues, en collaboration avec des climatologues, océanologues, mathématiciens et informaticiens. Un modèle numérique, basé sur des équations mathématiques, permet de simuler l'évolution des calottes polaires, notamment le vêlage d'icebergs. Des algorithmes résolvent les équations et sont mis en œuvre dans des logiciels informatiques.
Processus physiques en jeu dans un inlandsis
À l'intérieur
La glace est un fluide qui s’écoule sous l’effet de son propre poids. Elle coule beaucoup plus lentement que l’eau liquide, car ses caractéristiques sont différentes. En particulier, la glace est un fluide plastique, c’est-à-dire qu’elle se déforme en s’écoulant. Les propriétés physiques et mécaniques de la glace changent avec la pression et la température. Or la pression augmente avec la profondeur à cause du poids de la glace et la température, très froide en surface, augmente aussi avec la profondeur. Par conséquent, la vitesse du glacier varie en intensité et en direction à l’intérieur de la calotte polaire.
À la base
À la base, lorsque la glace est froide, elle adhère au socle rocheux et des forces de friction diminuent la vitesse. La température à la base comme à l’intérieur augmente avec le flux géothermique, qui est la chaleur apportée par la croûte terrestre. Lorsque la glace est à son point de fusion, 0°C, un film d’eau permet le glissement et augmente la vitesse. En Antarctique et au Groenland, les zones de plus fort glissement sont situées sur les côtes, dans des vallées ressemblant à des canyons ou à des fjords.
Ces fleuves de glace, appelés glaciers émissaires, ont des vitesses spectaculaires, supérieures à 10km/an.
En surface
En surface, de la glace s’ajoute à la glace existante à cause des précipitations et du regel de l’eau : c’est l’accumulation. Au contraire, de la glace disparaît, à cause de la fonte ou du vent : c’est l’ablation. Les conditions météorologiques et la température à la surface de la calotte influent sur la quantité de précipitations neigeuses, ainsi que sur la fonte et sur le transport par le vent, donc sur l’accumulation et l’ablation et par conséquent sur l’altitude du glacier. Lorsque la température de surface augmente à cause du réchauffement climatique, la glace fond et l’altitude diminue par ablation. Mais la température augmente lorsque l’altitude diminue, donc le glacier continue de fondre et de s’amincir. Le phénomène peut ainsi s'amplifier et la calotte disparaître rapidement.
Cette instabilité des petites calottes est un exemple de rétroaction, où une cause produit un effet qui agit en retour sur cette cause.
Au niveau de la mer
Les glaciers émissaires qui s’écoulent très rapidement perdent de grandes quantités de glace sous la forme d’icebergs et contribuent ainsi au changement du niveau des mers. Les plates-formes de glace flottante prolongent les calottes sur l’océan. Lorsque les eaux océaniques se réchauffent, ces plates-formes fondent par la base et modifient le niveau de l’océan.
Ce changement du niveau des mers influe à son tour sur la vitesse du glacier : on observe une rétroaction entre les différents processus physiques. En effet, le changement du niveau de la mer modifie la ligne d’échouage, là où la calotte se met à flotter. La géométrie de la plate-forme flottante et par voie de conséquence l’écoulement de glace sont modifiés.
Sélectionner une zone
Modèle mathématique
À l'intérieur
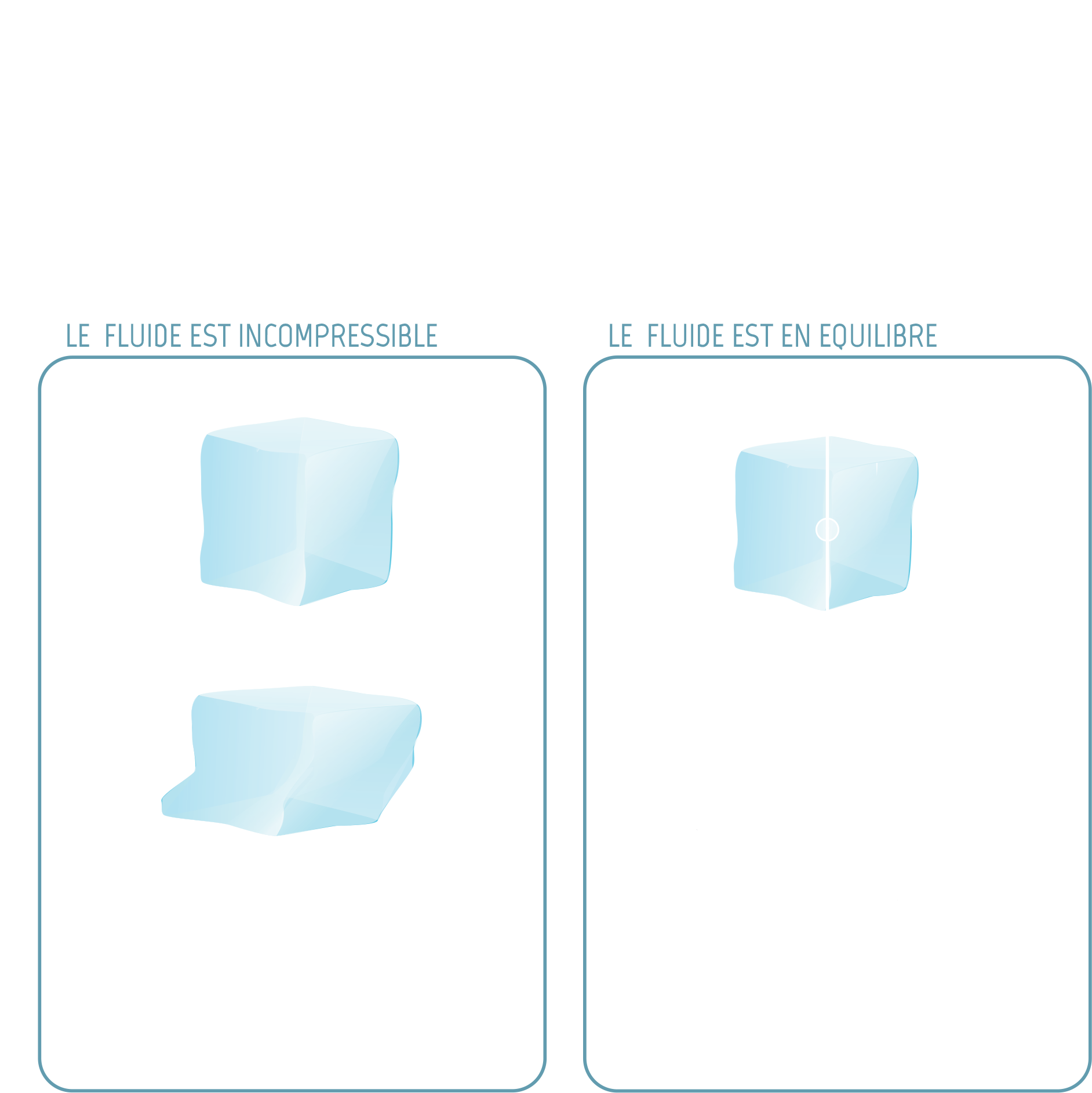
La glace s’écoule car c’est un fluide. Le modèle met en équations deux lois fondamentales de la physique. D’une part, la glace est un fluide incompressible, donc un petit glaçon se déforme en gardant le même volume et la même masse : c’est la loi de conservation de la masse. D’autre part, la glace est en équilibre, donc la somme des forces qui s’exercent sur un cube de glace est nulle : c’est la loi de conservation de la quantité de mouvement, ou deuxième loi de Newton, lorsque l’accélération est nulle.
Les forces qui s’exercent sur un petit glaçon sont dues à la gravité, à la pression et à la viscosité. Pour calculer la force de viscosité, il faut définir une relation entre la vitesse de déplacement et les contraintes mécaniques dues à la plasticité du fluide. Les glaciologues utilisent la loi de Glen, qui fait intervenir la température et qui modélise les caractéristiques des cristaux de glace.
Il faut aussi une équation pour définir la température à l’intérieur : c’est la loi de conservation de l’énergie, qui prend en compte le flux géothermique et la température de surface. En pratique, on calcule souvent la température séparément, avec un modèle simplifié.
On obtient ainsi un ensemble d’équations, dont les inconnues sont la vitesse du fluide (l’intensité et la direction) et la pression, partout dans le volume glaciaire. Ce système d’équations s’appelle les équations de Stokes, qui sont une version simplifiée des fameuses équations de Navier-Stokes, dont la résolution est mise à prix pour un million de dollars. Ces équations de Stokes décrivent des relations entre les variations dans chaque direction de l’espace de la vitesse et de la pression : ce sont des équations aux dérivées partielles.
À la base
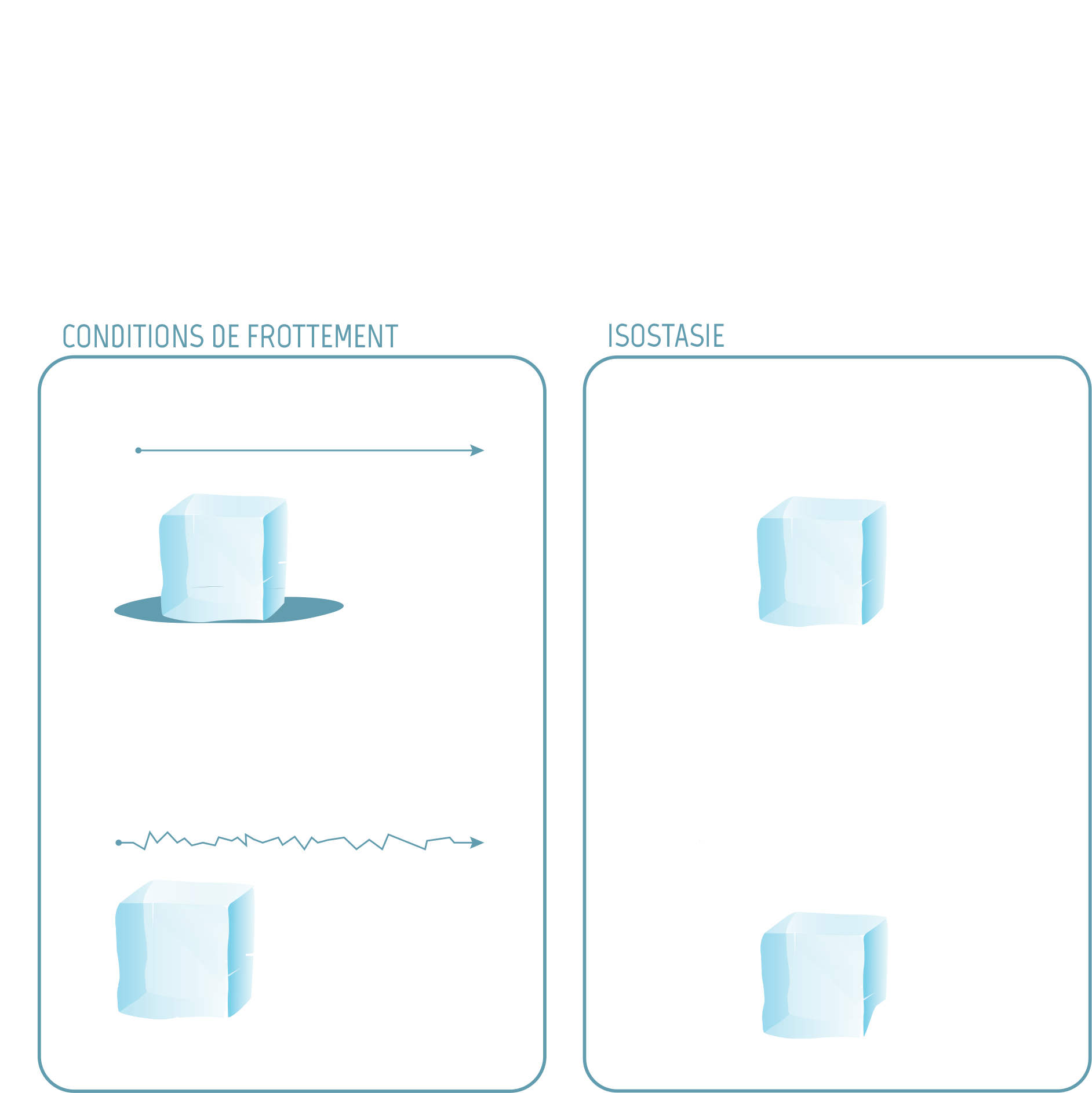
Les conditions de frottement et glissement sont complexes et sont souvent modélisées par une loi de friction (encore une équation avec des dérivées partielles) qui fait intervenir un coefficient de friction propre au glacier étudié. Ce coefficient varie en espace et est très difficile à mesurer.
De plus, l’altitude du socle peut varier. En effet, le socle rocheux s’enfonce lentement sous le poids de la glace et remonte lentement lorsque de la glace fond. Il y a une rétroaction entre le bilan de masse de surface, l’écoulement du glacier et l’altitude du socle. Ce rebond, appelé isostasie, se produit au bout d’environ 10 000 ans et peut donc être ignoré lorsqu’on étudie l’évolution de l’inlandsis durant un siècle.
En surface
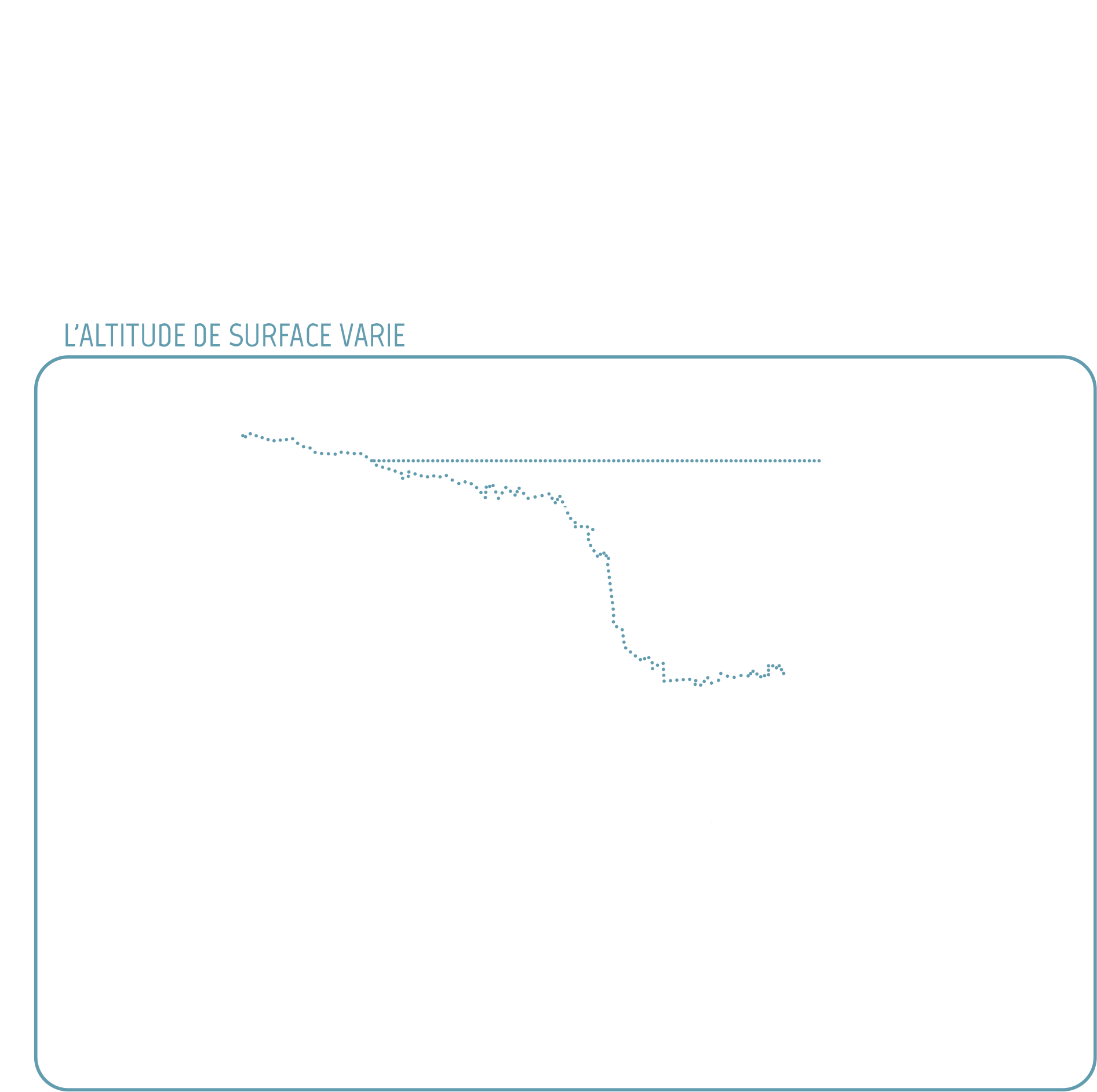
L’altitude de surface peut augmenter par accumulation ou décroître par ablation. Elle peut aussi varier à cause du mouvement du glacier. L’équation qui traduit l’évolution au cours du temps de l’altitude de surface est un bilan de masse de surface. L’accumulation et l’ablation sont calculées grâce à un modèle climatique, tandis que le changement dû au mouvement est calculé avec la vitesse de surface du glacier.
Le bilan de masse de surface est encore une équation aux dérivées partielles, avec non seulement des variations dans l’espace de l’altitude mais aussi une variation dans le temps.
Au niveau de la mer
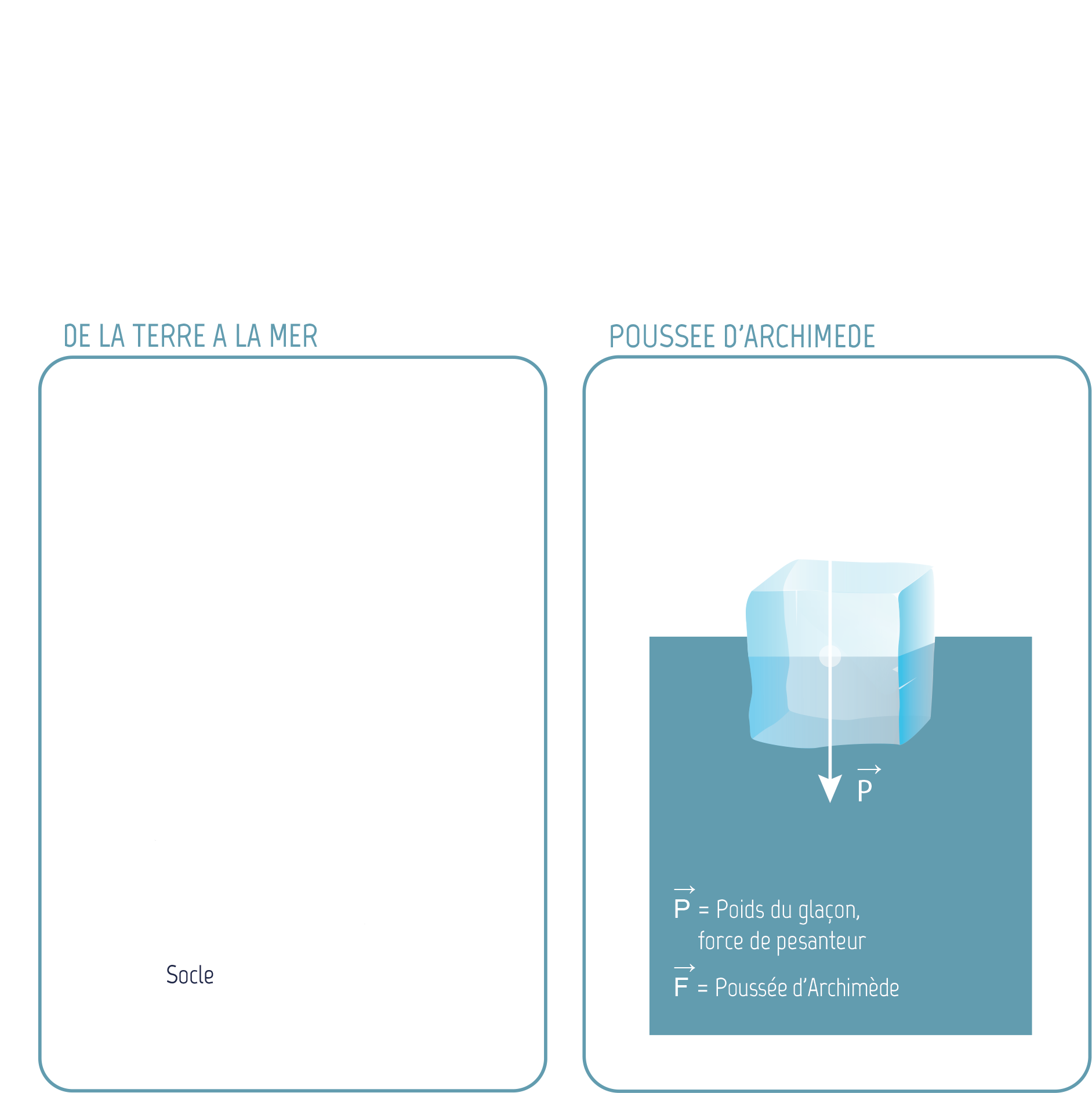
La ligne d’échouage correspond à l’endroit où la calotte polaire se met à flotter sur l’océan. La plate-forme flottante est soumise en plus à la poussée d’Archimède exercée par l’eau. Une équation traduit l’équilibre des forces pour la frontière entre la calotte polaire et l’océan, en tenant compte de la différence des masses volumiques entre la glace et l’eau.
Une équation porte aussi sur les autres frontières de la calotte polaire pour compléter le système.
Sélectionner une zone
Calcul de l’évolution d’un glacier
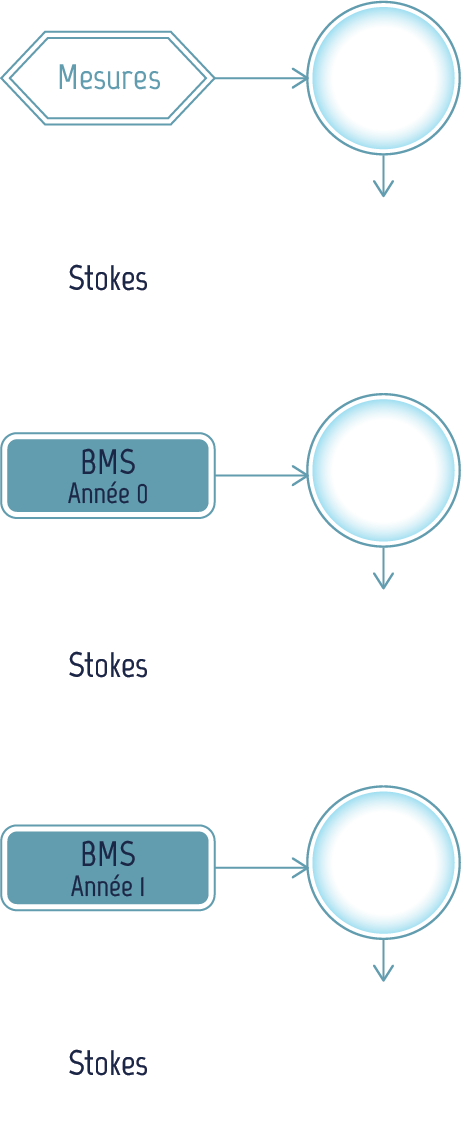
Pour déterminer l’évolution d’un glacier, il faut calculer l’altitude à des instants réguliers, par exemple tous les ans. Pour cela, il faut actualiser le Bilan de Masse de Surface (BMS), qui dépend de la vitesse et des conditions météorologiques. Il faut aussi recalculer la vitesse du glacier, qui dépend de l’altitude.
Connaissant grâce à des mesures l’altitude de surface pour l'année 0, on calcule la vitesse pour l'année 0, grâce aux équations de Stokes. On peut alors calculer le Bilan de Masse de Surface pour l’année 0 et on en déduit l’altitude de surface pour l’année 1.
On calcule alors la vitesse pour l’année 1, puis le Bilan de Masse de Surface, puis l’altitude de surface pour l’année 2, etc.
Calcul de la vitesse d'un glacier
Maillage du Groenland et vitesse simulée. Il y a plus de triangles dans les zones des glaciers émissaires pour calculer précisément les variations rapides de la vitesse.
Connaissant l’altitude de surface pour l'année n, on calcule la vitesse pour l'année n, en résolvant les équations aux dérivées partielles de Stokes.
La première étape est de passer des inconnues définies partout à des inconnues définies par un nombre fini de valeurs. Cette étape s’appelle une discrétisation spatiale. Pour cela, la surface du glacier est découpée en petits triangles, et l’épaisseur du glacier en tranches, ce qui aboutit à un découpage du volume glaciaire en petits glaçons ayant une forme de prisme, qu'on appelle des mailles.
Image d'après Gillet-Chaulet, F., Gagliardini, O., Seddik, H., Nodet, M., Durand, G., Ritz, C., Zwinger, T., Greve, R., and Vaughan, D. G.: Greenland ice sheet contribution to sea-level rise from a new-generation ice-sheet model, The Cryosphere, 6, 1561-1576, 2012. Licence CC-BY 3.0.
Résolution des équations de stokes
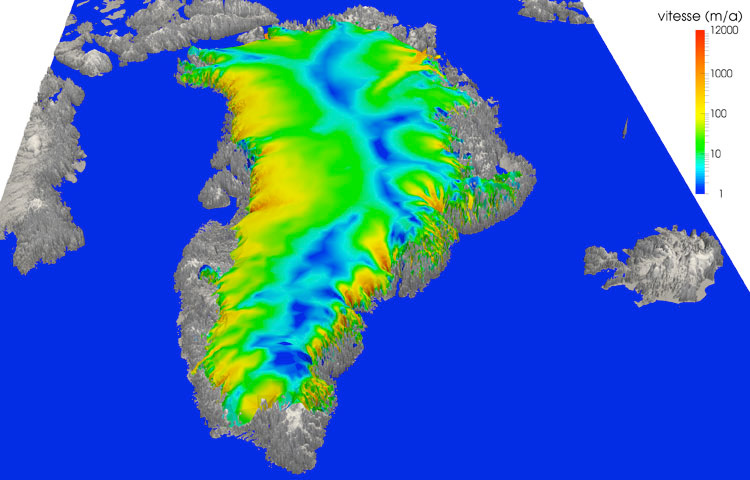
Vitesse simulée en 3D de la calotte polaire du Groenland. Les glaciers émissaires vont nettement plus vite (en rouge, 12 km par an) que les autres parties (en bleu, 1 m par an)
Image: Fabien Gillet-Chaulet, CNRS & LGGE, Grenoble.
Ensuite, les équations de Stokes sont transformées en un système d’équations algébriques (sans dérivée) compliquées, avec autant d’équations que d’inconnues. On ne sait pas résoudre de façon exacte un tel système, alors on utilise un algorithme itératif, qui procède par approximations successives. On contrôle mathématiquement l’erreur et on arrête l’algorithme lorsque celle-ci est assez petite.
Quiz
Pour simuler le mouvement d'un glacier, on réalise un maillage en découpant le volume en petits glaçons. Que se passe-t-il quand on diminue le nombre de glaçons ?
Non, la bonne réponse est la 2
Pour calculer la vitesse et l’altitude avec une bonne précision, il faut beaucoup de mailles, surtout dans les zones de forte vitesse. Mais le nombre d’équations augmente avec le nombre de mailles et le temps de calcul augmente avec le nombre d’équations. Comme dans la plupart des simulations numériques, il faut trouver un compromis entre la précision du résultat et le temps de calcul.
Bravo !
Pour calculer la vitesse et l’altitude avec une bonne précision, il faut beaucoup de mailles, surtout dans les zones de forte vitesse. Mais le nombre d’équations augmente avec le nombre de mailles et le temps de calcul augmente avec le nombre d’équations. Comme dans la plupart des simulations numériques, il faut trouver un compromis entre la précision du résultat et le temps de calcul.
Non, la bonne réponse est la 2
Pour calculer la vitesse et l’altitude avec une bonne précision, il faut beaucoup de mailles, surtout dans les zones de forte vitesse. Mais le nombre d’équations augmente avec le nombre de mailles et le temps de calcul augmente avec le nombre d’équations. Comme dans la plupart des simulations numériques, il faut trouver un compromis entre la précision du résultat et le temps de calcul.
Non, la bonne réponse est la 2
Pour calculer la vitesse et l’altitude avec une bonne précision, il faut beaucoup de mailles, surtout dans les zones de forte vitesse. Mais le nombre d’équations augmente avec le nombre de mailles et le temps de calcul augmente avec le nombre d’équations. Comme dans la plupart des simulations numériques, il faut trouver un compromis entre la précision du résultat et le temps de calcul.
